奇偶校验

校验位只有一位,根据编码长度中1的个数来确定这1位的数值
有两种校验方法：奇校验和偶校验,实际上是根据看奇数为1还是偶数为1,可以在接收端模2来校验
奇校验：原始码流+校验位 总共有奇数个1
偶校验：原始码流+校验位 总共有偶数个1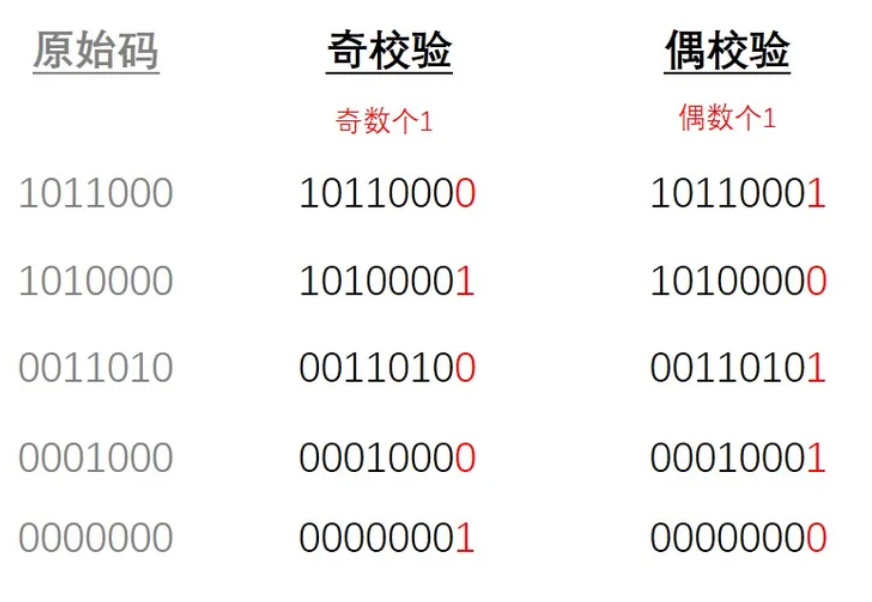

数学原理

编码的数学推导

模2除法

无进位的相加/无进位的相减/异或这些说的都是一个东西，以4bit长度为例

1
2
3
4

  1101
+ 1011
--------
  0110 

模2除法就是二进制除法，但是在相减时采用无进制相减

多项式代数和多项式除法

高等代数中的多项式代数知识

1
2

M/N=Q...R 

这里容易得到，R会比N幂次要低，就和整数除法m/n=q..r ，0<=r<n 一样

1. 除法规则-竖式除法
   每次消去余数最高项，直到余数最高次项小于除数
   !除法

编码算法

将二进制看成多项式,这里是整个crc想法来源.
比如
1101可以看成,从高到低的第i个数字为.因为网络序是大端序,高位先传输

设校验码+原信息长度共n位,其中校验码长度为k.在msg长度为n位的前提下，介绍一个除式,记作G(x),其最高项次数为k,并记原信息叫做S(x),最高项次数为n-k-1.

则根据多项式的带余除法,知一定存在一对唯一的P(x)和R(x)使得,其中R(x)的次数小于Q(x)的次数,存在性和唯一性对模2带余除法也成立(后面会做证明). 于是将原先的多项式带余除法推广到模2带余除法，自然就有

此时再令，这一步是关键,因为模2除法相加和相减结果是一样的,是可以被整除的，余式为0.即由,可得

于是当接收端收到数据后，再做

模2带余除法存在性和唯一性

存在性

因为与普通带余除法每区别，不管是无进位相减还是带进位相减，最终都会得到一个结果，故存在性比较显然

唯一性

设另外存在P(x)和T(x)，也满足条件.则有,因为

注意这里用的是模2加减法

能检测哪些错误

这里最主要的是一个建模,核心在这里。是沟通理论和实际的桥梁。接下来就是理论上的证明了.所以我们思考问题的时候，是需要去寻找理论中的概念和原理，并将其和实际对应起来.对于包含错误的bit流可以看成

如果,则表示存在错误.如果选择的G(x)能够使下面命题成立,则表示可以检测出错误.

当余数为0等价于E(x)为0 …(命题1)

E(x)不为0时等价余数不为0 …(命题2)

解释：余数为0也可能是G(x)整除E(x).命题1和命题2也是等价的

定理1

如果G(x)至少有2项,则可以检测出所有的单bit错误
证明: 单bit错误表示,那么只有当G(x)形如时才E(x)会被整除。只要G(x)至少有2项那么就无法整除E(x). 命题1成立

定理2

如果是G(x)因式,则可以被检测所有的奇数个bit错误
证明:假定通过G(x)生成的编码信息为F(x),

则
其中 ,

令x=1可得,

故F(1)一定是偶数,F(x)又是多项式,故F(x)一定有偶数项.所以当发生奇数个错误时余式一定不为0.命题2成立

剩下的定理

原论文中总共给出了8条定理,目前水平有限,等待后续领悟。

原论文

原论文是大牛Peterson在1961年发布的论文Cyclic Code for Error Detection.

crc碰撞

这里介绍2个单词,在编码领域会经常要讨论的一个问题.冲突概率conflict collisions.我之前其实一直想不通,既然会有概率冲突，为啥还可以用来做校验呢？

后面我想明白了，加密安全和传输校验不一样，信息传输过程中即使碰到了冲突也是可以接受的，接收端就认为这是源端发送的数据。但是当校验错误，接收端就要求源端重新发送。还有一个特性就是，信道一般发生错误集中在某一段内，不会产生各种各样的花式错误.

就像md5一样，虽然大家一直在用，但md5也会有冲突，愿意使用就表示接受冲突带来的结果。md5由我国的王小云院士优化了破解算法md5冲突王院士,感兴趣的同学可以看下王院士的主页.

碰撞分析

这块涉及到比较复杂的数学知识，留作自己后续的研究方向.

常用的除数多项式

所以检测错误的能力和选择多项式的特性有关，不是随便瞎选的
见wiki常用的多项式

算法实现

1. 朴素的竖式多项式除法的翻译
   这里主要思路是用商消去最高位，然后在输入的数组上减去商*生成多项式，因此余数也是保存在输入的被除多项式位置

   1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32

   int divide( double num[], int nlen, double den[], int dlen, double quotient[], int *qlen ) { int n, d, q; // The lengths are one more than the last index; decrement them // here so the call is less confusing nlen--; dlen--; q = 0; // when n > dlen, the result is no longer a polynomial // (e.g. trying to divide x by x^2) for ( n = nlen; n >= dlen; n-- ) { // First, divide the nth element of numerator with the last element // of the denominator quotient[ n - dlen ] = num[ n ] / den[ dlen ]; q++; // Now, multiply each element of the denominator by each // corresponding element of the numerator and subtract the // result for ( d = dlen; d >= 0; d-- ) { num[ n - ( dlen - d ) ] -= den[ d ] * quotient[ n - dlen ]; //采用模2除法，需要修改成这行代码 num[ n - ( denlen - d ) ] = fabs( num[ n - ( denlen - d ) ] ); } } *qlen = q; return ( nlen - *qlen + 1 ); }

2. 使用异或来计算
   这里比较难理解，让我想了很久，还是基于竖式除法的思路，从竖式除法我们可以发现，32位的生成多项式最高位可以不存储，因为每次都是消去最高项；可以用一个32位int来保存余数，长度小于32位的二进制序列余数就是它自己，因此需要在右端补上32位；从竖式除法中我们可以发现，做减法的次数等于被除数长度-除数长度+1；

   1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24

   unsigned long int compute_crc( unsigned long input, int len, unsigned long divisor ) { //要做被除数长度-除数长度+1=24+32-33+1=24 while ( len-- ) { //如果最高位是1，那么这位是要被消去，余数等于剩下的和除数异或；如果最高位是0，我们发现最高位死0，实际上是 //商为0，和全0异或等于它自己，等效于直接左移 input = ( input & 0x80000000 ) ? divisor ^ ( input << 1 ) : ( input << 1 ); } //余数存储在32位，这里实际上等价于竖式多项式的低32位；因为运算过程中，余数始终保存在input位置 return input; } ... unsigned long int crc32_divisor = 0x04C11DB7; //下面的input按ABC实际上的值字节做了反转，多项式是低字节在低位，为了位对齐 // 0.0, 1.0, 0.0, 0.0, 0.0, 0.0, 1.0, 1.0, // C // 0.0, 1.0, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0, // B // 0.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0 // A unsigned long int input = 0x8242C200; // ABC; backwards & left aligned printf( "%lx\n", compute_crc( input, 24, crc32_divisor ); // 5A5B433A

crc查表法

https://www.cnblogs.com/esestt/archive/2007/08/09/848856.html

常见组件关于crc的实现

1. mariadb中用的是查表，或者使用cpu的sse来计算
   mariadb crc
2. gcc中zlib
   gcc中zlib

引用

1. 这是大牛的ppt讲解
2. crc原论文
3. 多项式除法
4. 模2除法
5. crc32校验和
6. 更详细的crc doc

哈希表

是一种kv的数据结构，插入查找都是O(1)的

哈希函数

用来生成key的哈希值的函数,一般都是根据类成员的哈希值再相加

jdk中的HashMap

哈希表的一种实现,插入和查找都是依据 key的哈希函数生成的哈希值来确定位置的。冲突时使用的是拉链法

put

主要流程:

1. 调用哈希函数获取哈希值，对数组长度取余，找到对应的桶。
   如果桶中无元素，直接放入
   如果桶中有元素，再看是否和当前元素和已有元素是否相同，
   如果相同，则覆盖原有的值
   如果不相同，则使用拉链法，在链表尾部插入一个节点或者把链表变成树

下面结合代码来解释：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66

 static final int hash(Object key) {
         int h;
         return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
     }

public V put(K key, V value) {
     return putVal(hash(key), key, value, false, true);
 }

 /**
  * Implements Map.put and related methods.
  *
  * @param hash hash for key
  * @param key the key
  * @param value the value to put
  * @param onlyIfAbsent if true, don't change existing value
  * @param evict if false, the table is in creation mode.
  * @return previous value, or null if none
  */
 final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
                boolean evict) {
     Node<K,V>[] tab; Node<K,V> p; int n, i;
     if ((tab = table) == null || (n = tab.length) == 0)//如果还没有初始化数组,则初始化一个
         n = (tab = resize()).length;
     if ((p = tab[i = (n - 1) & hash]) == null)//如果对应的桶处没有元素,则创建一个
         tab[i] = newNode(hash, key, value, null);
     else {
         Node<K,V> e; K k;
         //p是对应桶处的元素,这里是在判断是否是同一个key
         if (p.hash == hash &&
             ((k = p.key) == key || (key != null && key.equals(k))))
             e = p;
         else if (p instanceof TreeNode)
             e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
         else {
             //冲突的元素，链表法或者转成树(一般不会走到)
             for (int binCount = 0; ; ++binCount) {
                 if ((e = p.next) == null) {
                     //在最后面加上一个节点
                     p.next = newNode(hash, key, value, null);
                     if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
                         treeifyBin(tab, hash);
                     break;
                 }
                 if (e.hash == hash &&
                     ((k = e.key) == key || (key != null && key.equals(k))))
                     break;
                 p = e;
             }
         }
         //如果相同，则覆盖原有的值
         if (e != null) { // existing mapping for key
             V oldValue = e.value;
             if (!onlyIfAbsent || oldValue == null)
                 e.value = value;
             afterNodeAccess(e);
             return oldValue;
         }
     }
     ++modCount;
     //如果达到阈值则扩容
     if (++size > threshold)
         resize();
     afterNodeInsertion(evict);
     return null;
 }

get

主要流程是

1. 先用哈希函数找到对应的桶，如果已经存在，再遍历链表或者树
   下面结合代码来解释：

   1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24

   public V get(Object key) { Node<K,V> e; return (e = getNode(hash(key), key)) == null ? null : e.value; } final Node<K,V> getNode(int hash, Object key) { Node<K,V>[] tab; Node<K,V> first, e; int n; K k; if ((tab = table) != null && (n = tab.length) > 0 && (first = tab[(n - 1) & hash]) != null) { if (first.hash == hash && // always check first node ((k = first.key) == key || (key != null && key.equals(k)))) return first; if ((e = first.next) != null) { if (first instanceof TreeNode) return ((TreeNode<K,V>)first).getTreeNode(hash, key); do { if (e.hash == hash && ((k = e.key) == key || (key != null && key.equals(k)))) return e; } while ((e = e.next) != null); } } return null; }

扩容

主要流程

1. 扩容大小为原来2倍，更新阈值为容量*loadFactor
2. 找到在新数组中的位置,这个有个简单的数学原理
   由于扩容是总是扩容2倍，一开始大小也是2的幂次，故大小总是为2的幂次
   设当前大小为newsize，则
   hash % newsize = hash & (newsize-1); 因为比newsize低的位都会是余数的位。
   更进一步,设某个桶在原数组中下标为x，在新数组中下标为y，原数组大小为oldsize,则x,y满足

   1 2 3 4 5 6

   hash % oldsize=x if (hash & oldsize ==1 ){ y = x + oldsize//分支1 }else{ y = x//分支2 }

   原因还是因为比数组大小低的位哪些会对余数产生贡献。

根据上面原理，在拷贝原数组的元素时，只需要将桶后面的链表拆分成2部分，一部分属于分支1，一部分属于分支2，放入对应的桶中即可
下面结合代码来解释

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78

final Node<K,V>[] resize() {
       Node<K,V>[] oldTab = table;
       int oldCap = (oldTab == null) ? 0 : oldTab.length;
       int oldThr = threshold;
       int newCap, newThr = 0;
       if (oldCap > 0) {
           if (oldCap >= MAXIMUM_CAPACITY) {
               threshold = Integer.MAX_VALUE;
               return oldTab;
           }
           else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY &&
                    oldCap >= DEFAULT_INITIAL_CAPACITY)
               newThr = oldThr << 1; // double threshold
       }
       else if (oldThr > 0) // initial capacity was placed in threshold
           newCap = oldThr;
       else {               // zero initial threshold signifies using defaults
           newCap = DEFAULT_INITIAL_CAPACITY;
           newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);
       }
       if (newThr == 0) {
           float ft = (float)newCap * loadFactor;
           newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ?
                     (int)ft : Integer.MAX_VALUE);
       }
       threshold = newThr;
       @SuppressWarnings({"rawtypes","unchecked"})
       Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap];
       table = newTab;
       if (oldTab != null) {
           for (int j = 0; j < oldCap; ++j) {
               Node<K,V> e;
               if ((e = oldTab[j]) != null) {
                   oldTab[j] = null;
                   if (e.next == null)
                       newTab[e.hash & (newCap - 1)] = e;
                   else if (e instanceof TreeNode)
                       ((TreeNode<K,V>)e).split(this, newTab, j, oldCap);
                   else { // preserve order
                   //将原来的链表拆分成2部分,先叫做low和high吧
                       Node<K,V> loHead = null, loTail = null;
                       Node<K,V> hiHead = null, hiTail = null;
                       Node<K,V> next;

                       do {
                           next = e.next;
                           //根据最后一位来判断是要放入low部分还high部分
                           if ((e.hash & oldCap) == 0) {
                               if (loTail == null)
                                   loHead = e;
                               else
                                   loTail.next = e;
                               loTail = e;
                           }
                           else {
                               if (hiTail == null)
                                   hiHead = e;
                               else
                                   hiTail.next = e;
                               hiTail = e;
                           }
                       } while ((e = next) != null);
                       // //把low部分的链表头部放入 newTab[j]位置
                       if (loTail != null) {
                           loTail.next = null;
                           newTab[j] = loHead;
                       }
                       //把high部分的链表头部放入 newTab[j + oldCap]位置
                       if (hiTail != null) {
                           hiTail.next = null;
                           newTab[j + oldCap] = hiHead;
                       }
                   }
               }
           }
       }
       return newTab;
   }

jdk线程安全容器

在多线程环境下,向容器插入删除数据依旧保持正确性,不会出现逻辑错误

线程安全的哈希表

ConcurrentHashMap

put

主要流程:

1. 如果没有初始化，则初始化数组
2. 根据hashcode找到桶的位置,查看是否为空,如果为空,cas尝试一下.
   如果不为空,则看整个hashmap是否处于扩容拷贝数据状态,进入帮助拷贝数据
   如果未处于扩容拷贝数据状态,则对桶位置对象加锁,把元素加到链表中
3. 最后增加哈希表的元素数量(算法和LongAdder类似)

下面结合代码来解释

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129

 final V putVal(K key, V value, boolean onlyIfAbsent) {
        if (key == null || value == null) throw new NullPointerException();
        int hash = spread(key.hashCode());
        int binCount = 0;
        for (Node<K,V>[] tab = table;;) {
            Node<K,V> f; int n, i, fh; K fk; V fv;
            if (tab == null || (n = tab.length) == 0)
                tab = initTable();
                //先检查桶位置是否有元素
            else if ((f = tabAt(tab, i = (n - 1) & hash)) == null) {
                if (casTabAt(tab, i, null, new Node<K,V>(hash, key, value)))
                    break;                   // no lock when adding to empty bin
            }
            else if ((fh = f.hash) == MOVED)
                tab = helpTransfer(tab, f);
            else if (onlyIfAbsent // check first node without acquiring lock
                     && fh == hash
                     && ((fk = f.key) == key || (fk != null && key.equals(fk)))
                     && (fv = f.val) != null)
                return fv;
            else {
                V oldVal = null;
                //对桶对象加锁
                synchronized (f) {
                    if (tabAt(tab, i) == f) {
                        if (fh >= 0) {
                            binCount = 1;
                            for (Node<K,V> e = f;; ++binCount) {
                                K ek;
                                if (e.hash == hash &&
                                    ((ek = e.key) == key ||
                                     (ek != null && key.equals(ek)))) {
                                    oldVal = e.val;
                                    if (!onlyIfAbsent)
                                        e.val = value;
                                    break;
                                }
                                Node<K,V> pred = e;
                                if ((e = e.next) == null) {
                                    pred.next = new Node<K,V>(hash, key, value);
                                    break;
                                }
                            }
                        }
                        else if (f instanceof TreeBin) {
                            Node<K,V> p;
                            binCount = 2;
                            if ((p = ((TreeBin<K,V>)f).putTreeVal(hash, key,
                                                           value)) != null) {
                                oldVal = p.val;
                                if (!onlyIfAbsent)
                                    p.val = value;
                            }
                        }
                        else if (f instanceof ReservationNode)
                            throw new IllegalStateException("Recursive update");
                    }
                }
                if (binCount != 0) {
                    if (binCount >= TREEIFY_THRESHOLD)
                        treeifyBin(tab, i);
                    if (oldVal != null)
                        return oldVal;
                    break;
                }
            }
        }
        //增加元素个数
        addCount(1L, binCount);
        return null;
    }
    //拷贝数据函数
        final Node<K,V>[] helpTransfer(Node<K,V>[] tab, Node<K,V> f) {
        Node<K,V>[] nextTab; int sc;
        if (tab != null && (f instanceof ForwardingNode) &&
            (nextTab = ((ForwardingNode<K,V>)f).nextTable) != null) {
            int rs = resizeStamp(tab.length);
            while (nextTab == nextTable && table == tab &&
                   (sc = sizeCtl) < 0) {
                if ((sc >>> RESIZE_STAMP_SHIFT) != rs || sc == rs + 1 ||
                    sc == rs + MAX_RESIZERS || transferIndex <= 0)
                    break;
                if (U.compareAndSetInt(this, SIZECTL, sc, sc + 1)) {
                    transfer(tab, nextTab);
                    break;
                }
            }
            return nextTab;
        }
        return table;
    }
//主要是利用求和可以分散到多个int变量上
private final void addCount(long x, int check) {
        CounterCell[] cs; long b, s;
        if ((cs = counterCells) != null ||
            !U.compareAndSetLong(this, BASECOUNT, b = baseCount, s = b + x)) {
            CounterCell c; long v; int m;
            boolean uncontended = true;
            if (cs == null || (m = cs.length - 1) < 0 ||
                (c = cs[ThreadLocalRandom.getProbe() & m]) == null ||
                !(uncontended =
                  U.compareAndSetLong(c, CELLVALUE, v = c.value, v + x))) {
                fullAddCount(x, uncontended);
                return;
            }
            if (check <= 1)
                return;
            s = sumCount();
        }
        if (check >= 0) {
            Node<K,V>[] tab, nt; int n, sc;
            while (s >= (long)(sc = sizeCtl) && (tab = table) != null &&
                   (n = tab.length) < MAXIMUM_CAPACITY) {
                int rs = resizeStamp(n);
                if (sc < 0) {
                    if ((sc >>> RESIZE_STAMP_SHIFT) != rs || sc == rs + 1 ||
                        sc == rs + MAX_RESIZERS || (nt = nextTable) == null ||
                        transferIndex <= 0)
                        break;
                    if (U.compareAndSetInt(this, SIZECTL, sc, sc + 1))
                        transfer(tab, nt);
                }
                else if (U.compareAndSetInt(this, SIZECTL, sc,
                                             (rs << RESIZE_STAMP_SHIFT) + 2))
                    transfer(tab, null);
                s = sumCount();
            }
        }
    }

get

主要流程:

1. 根据hashcode计算得到桶的位置
2. 在链表中或者树上查找是否相等
   下面结合代码来解释

   1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

   public V get(Object key) { Node<K,V>[] tab; Node<K,V> e, p; int n, eh; K ek; int h = spread(key.hashCode()); if ((tab = table) != null && (n = tab.length) > 0 && (e = tabAt(tab, (n - 1) & h)) != null) { if ((eh = e.hash) == h) { if ((ek = e.key) == key || (ek != null && key.equals(ek))) return e.val; } else if (eh < 0) return (p = e.find(h, key)) != null ? p.val : null; while ((e = e.next) != null) { if (e.hash == h && ((ek = e.key) == key || (ek != null && key.equals(ek)))) return e.val; } } return null; }

扩容

主要流程

1. 计算每个线程拷贝的元素的个数,最少是拷贝MIN_TRANSFER_STRIDE(16)个
2. 有个全局的volatile 变量transferIndex,记录者前面线程领取的元素,从数组后面开始向前领取任务,领取完修改transferIndex
3. 将新数组的桶的位置设置成ForwardingNode,告诉其他线程现在正在扩容.
4. 拷贝桶链表和数的元素和hash表一样,分高低位
   下面结合代码来解释

   1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137

   private final void transfer(Node<K,V>[] tab, Node<K,V>[] nextTab) { int n = tab.length, stride; // if ((stride = (NCPU > 1) ? (n >>> 3) / NCPU : n) < MIN_TRANSFER_STRIDE) stride = MIN_TRANSFER_STRIDE; // subdivide range if (nextTab == null) { // initiating try { @SuppressWarnings("unchecked") Node<K,V>[] nt = (Node<K,V>[])new Node<?,?>[n << 1]; nextTab = nt; } catch (Throwable ex) { // try to cope with OOME sizeCtl = Integer.MAX_VALUE; return; } nextTable = nextTab; //从n到0 transferIndex = n; } int nextn = nextTab.length; ForwardingNode<K,V> fwd = new ForwardingNode<K,V>(nextTab); boolean advance = true; boolean finishing = false; // to ensure sweep before committing nextTab for (int i = 0, bound = 0;;) { Node<K,V> f; int fh; while (advance) { int nextIndex, nextBound; if (--i >= bound || finishing) advance = false; else if ((nextIndex = transferIndex) <= 0) { i = -1; advance = false; } //领取任务并修改transferIndex else if (U.compareAndSetInt (this, TRANSFERINDEX, nextIndex, nextBound = (nextIndex > stride ? nextIndex - stride : 0))) { bound = nextBound; i = nextIndex - 1; advance = false; } } if (i < 0 || i >= n || i + n >= nextn) { int sc; if (finishing) { nextTable = null; table = nextTab; sizeCtl = (n << 1) - (n >>> 1); return; } if (U.compareAndSetInt(this, SIZECTL, sc = sizeCtl, sc - 1)) { if ((sc - 2) != resizeStamp(n) << RESIZE_STAMP_SHIFT) return; finishing = advance = true; i = n; // recheck before commit } } //如果桶的位置为空,设置成ForwardingNode else if ((f = tabAt(tab, i)) == null) advance = casTabAt(tab, i, null, fwd); else if ((fh = f.hash) == MOVED) advance = true; // already processed else { synchronized (f) { if (tabAt(tab, i) == f) { Node<K,V> ln, hn; //拆分成高低位 if (fh >= 0) { int runBit = fh & n; Node<K,V> lastRun = f; for (Node<K,V> p = f.next; p != null; p = p.next) { int b = p.hash & n; if (b != runBit) { runBit = b; lastRun = p; } } if (runBit == 0) { ln = lastRun; hn = null; } else { hn = lastRun; ln = null; } for (Node<K,V> p = f; p != lastRun; p = p.next) { int ph = p.hash; K pk = p.key; V pv = p.val; if ((ph & n) == 0) ln = new Node<K,V>(ph, pk, pv, ln); else hn = new Node<K,V>(ph, pk, pv, hn); } setTabAt(nextTab, i, ln); setTabAt(nextTab, i + n, hn); setTabAt(tab, i, fwd); advance = true; } else if (f instanceof TreeBin) { TreeBin<K,V> t = (TreeBin<K,V>)f; TreeNode<K,V> lo = null, loTail = null; TreeNode<K,V> hi = null, hiTail = null; int lc = 0, hc = 0; for (Node<K,V> e = t.first; e != null; e = e.next) { int h = e.hash; TreeNode<K,V> p = new TreeNode<K,V> (h, e.key, e.val, null, null); if ((h & n) == 0) { if ((p.prev = loTail) == null) lo = p; else loTail.next = p; loTail = p; ++lc; } else { if ((p.prev = hiTail) == null) hi = p; else hiTail.next = p; hiTail = p; ++hc; } } ln = (lc <= UNTREEIFY_THRESHOLD) ? untreeify(lo) : (hc != 0) ? new TreeBin<K,V>(lo) : t; hn = (hc <= UNTREEIFY_THRESHOLD) ? untreeify(hi) : (lc != 0) ? new TreeBin<K,V>(hi) : t; setTabAt(nextTab, i, ln); setTabAt(nextTab, i + n, hn); setTabAt(tab, i, fwd); advance = true; } } } } } }